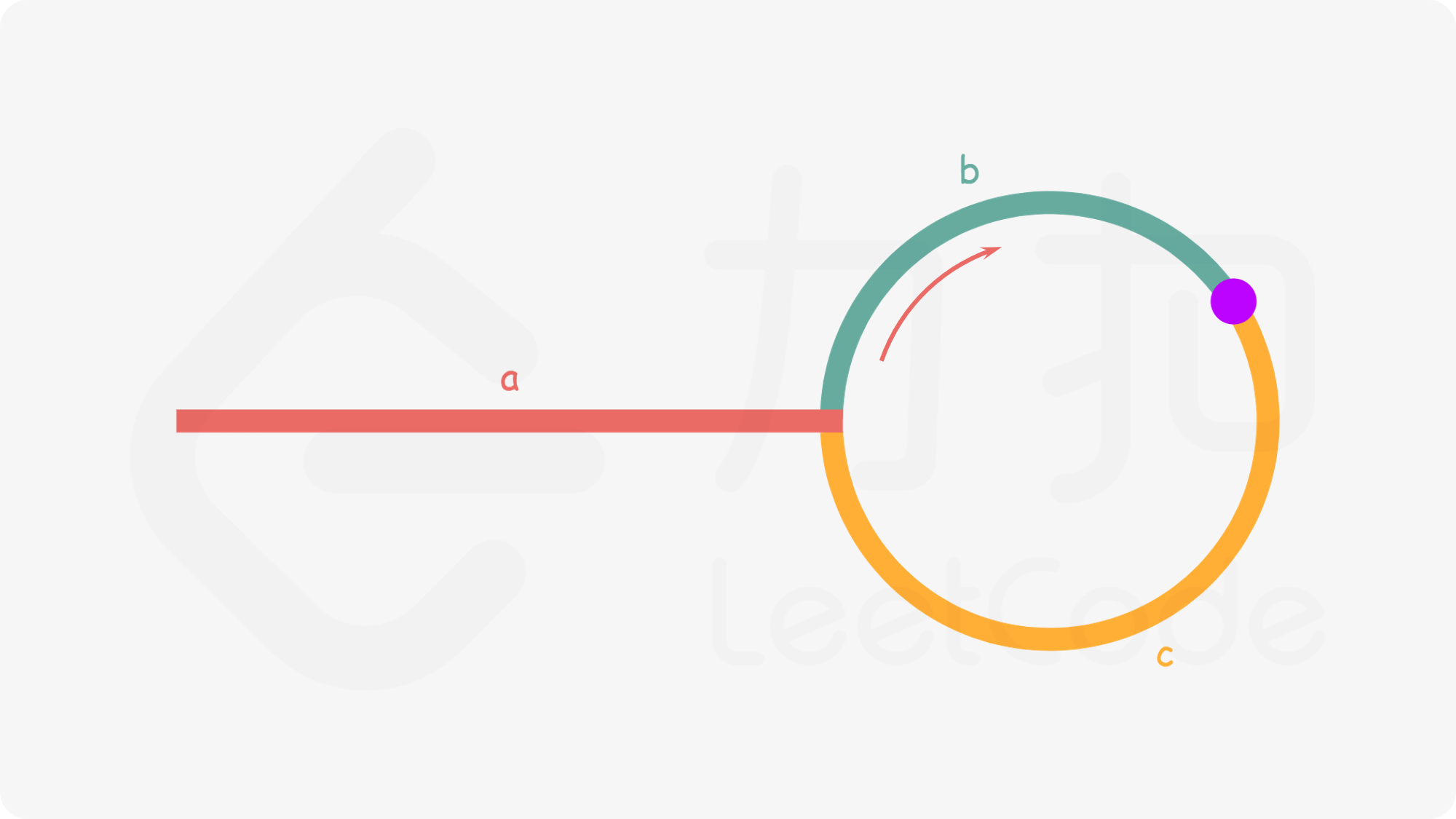力扣刷题笔记（二）

Foolish-Han Lv3
  2025-03-28 23:07:28 2025-03-28 23:07:28 创建   2025-04-21 18:16:25 2025-04-21 18:16:25 更新    3.9k 字  15 分钟  

跟着教程做了七道链表相关的题目，顿觉豁然开朗、天地宽广，未曾料想到如此简单的链表也会衍生出如此丰富的变化。虽不过是一些简单的奇技淫巧，却能在意想不到的地方起到非常的作用。

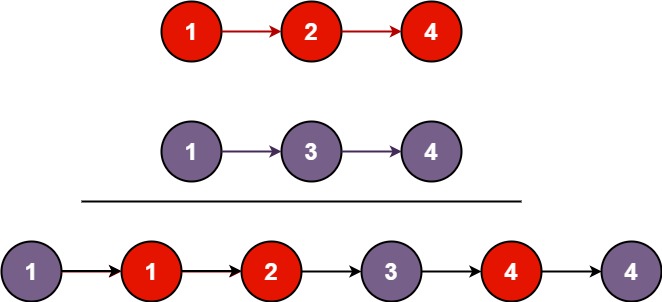
合并两个有序链表 - 21

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有结点组成的。

img
img

这道题是个开胃菜，没有什么难度。我们只需要在两个链表上各放一个指针，顺次向后便利进行合并即可。

不过我最初似乎错误理解了题意，这个题让“合并”链表，意即原链表是可以修改的。我则是把每个结点都复制了一遍构成了一个全新的链表，造成了不必要的空间开销。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        ListNode * l1 = list1;
        ListNode * l2 = list2;
        ListNode * dummy = new ListNode();
        ListNode * cur = dummy;
        while (l1 && l2) {
            if (l1->val < l2->val) {
                cur->next = l1;
                l1 = l1->next;
            } else {
                cur->next = l2;
                l2 = l2->next;
            }
            cur = cur->next;
        }
        if (l1) {
            cur->next = l1;
        }
        if (l2) {
            cur->next = l2;
        }
        ListNode * res = dummy->next;
        delete dummy;
        return res;
    }
};

注意到，这里使用了 dummy 这个虚拟头结点用于简化代码。因为我们不清楚两个链表中哪个头结点应该在前面，所以我们用 dummy 作为头结点使得原链表的头结点一般化，从而避免不必要的特判操作。这种做法后面还会看到。

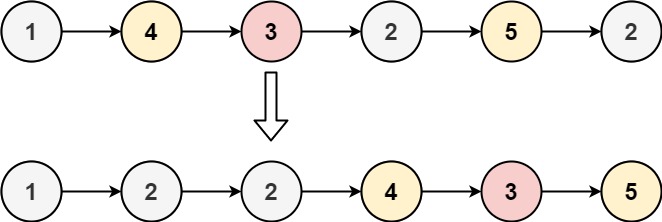
分隔链表 - 86

给你一个链表的头结点 head 和一个特定值 x ，请你对链表进行分隔，使得所有 小于 x 的结点都出现在 大于或等于 x 的结点之前。

你应当 保留 两个分区中每个结点的初始相对位置。

img
img

这个题也非常明确，我们只需要一个 l 指针记录当前结果链表中小于的结点中最后一个结点的位置，用 r 记录向右探索到的结点的位置，在符号要求时将 r 转移到 l 后面即可。

在这里，我仍然使用了虚拟头结点 dummy。这是因为，当我们需要把结点从一个位置转移到另一个位置时，这实际上需要进行删除和插入两个操作，删除时需要拿到待删除结点的前一个结点，插入时也需要拿到待插入位置的前一个结点。这时，就很容易遇到前一个结点并不存在的情况，需要特判。为了避免这种操作，我们就需要加一个虚拟头结点将其一般化，使得“前一个结点”永远存在。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* partition(ListNode* head, int x) {
        ListNode* dummy = new ListNode(-1000, head);
        ListNode* l = dummy;
        while (l->next && l->next->val < x) {
            l = l->next;
        }
        ListNode* r = l;
        while (r->next) {
            if (r->next->val < x) {
                ListNode* mv = r->next;
                r->next = mv->next;
                mv->next = l->next;
                l->next = mv;
                l = mv;
            } else {
                r = r->next;
            }
        } 
        ListNode* res = dummy->next;
        delete dummy;
        return res;
    }
};

当然，上面的思路实际上是要在一条链表中完成各项操作，所以略显麻烦，要考虑的点比较多。我们也可以用原链表生成两条链表，一条均为小于的，一条均为大于等于的，最后将其合并即可。这样，我们只需要进行将结点插入到新链表的尾部的操作即可。当然，我们要记得将最后一个结点的 next 置位空，避免循环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    ListNode* partition(ListNode* head, int x) {
        ListNode* dummy1 = new ListNode();
        ListNode* dummy2 = new ListNode();
        ListNode* p1 = dummy1, *p2 = dummy2;
        ListNode* p = head;
        while (p != nullptr) {
            if (p->val >= x) {
                p2->next = p;
                p2 = p2->next;
            } else {
                p1->next = p;
                p1 = p1->next;
            }
            p = p->next;
        }
        p1->next = dummy2->next;
		p2->next = nullptr;
        
        ListNode * res = dummy1->next;
        delete dummy1;
        delete dummy2;
        return res;
    }
};

合并 K 个升序链表 - 23

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

这个题相当于是第一个题的升级版，我之前曾经刷到过，但在第二次看到时我最先想到的仍然是分治。

但实际上，由于各个链表的长度分布并不均匀，合并两个链表的代价差异很大，所以分治算法的复杂度并不稳定。假设每个链表的长度均为，则有递归方程，复杂度为，即分治算法的最佳复杂度为，其中为结点的总数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class Solution
{
public:
    ListNode *mergeKLists(vector<ListNode *> &lists)
    {
        size_t size = lists.size();
        if (size == 0)
        {
            return nullptr;
        }
        if (size == 1)
        {
            return lists[0];
        }
        size_t mid = size / 2;
        vector<ListNode *> list_left(lists.begin(), lists.begin() + mid);
        vector<ListNode *> list_right(lists.begin() + mid, lists.end());
        ListNode *left = mergeKLists(list_left);
        ListNode *right = mergeKLists(list_right);
        ListNode *result = new ListNode(0);
        ListNode *p = result;
        while (left && right)
        {
            if (left->val < right->val)
            {
                result->next = left;
                left = left->next;
            }
            else
            {
                result->next = right;
                right = right->next;
            }
            result = result->next;
        }
        result->next = left ? left : right;
        result = p->next;
        delete p;
        return result;
    }
};

为了解决这个长度不一致的问题，我们该怎么做呢？答案是化整为零。我们将结点取出来，添加到优先队列中，然后再取出来构造合并后的链表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        auto cmp = [](ListNode* l, ListNode* r) -> bool {
            return l->val > r->val;
        };
        priority_queue<ListNode*, vector<ListNode*>, decltype(cmp)> pq;

        for (auto list: lists) {
            if (list) {
                pq.push(list);
            }
        }

        ListNode* head = new ListNode();
        ListNode* cur = head;

        while(!pq.empty()) {
            cur->next = pq.top();
            pq.pop();
            cur = cur->next;
            if (cur->next) {
                pq.push(cur->next);
            }
        }
        cur->next = nullptr;

        auto res = head->next;
        delete head;
        return res;
    }
};

可以看到，队列中的元素个数不超过，对所有结点都进行了一次添加删除操作，则有相当稳定的的复杂度。

值得注意的是，我在最初做的时候，一开始是把所有结点都加入队列，然后再一个个取出。这样做并没有利用每个链表原来已经是升序的性质，实际上把复杂度变为。我们合并个升序链表，实际上是要判断出哪个链表的首元素最小，然后把它添加到结果链表的尾部。采用优先队列正是为了帮我们简化找最小元素的操作。

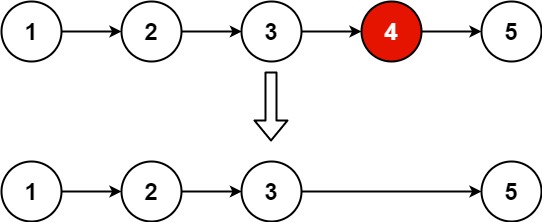
删除链表的倒数第个结点 - 19

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

img
img

从这道题开始，就有点脑筋急转弯的意思了。

假设链表共有个结点，那么删除倒数第个结点也即删除整数第个结点（注意这个加一）。因此，我们需要先遍历一遍链表获取其长度，接着再遍历一遍去删除第个结点。问题来了，我们能不能只遍历一遍？答案是肯定的。

由于要删除倒数第个结点，所以我们要找到倒数第个结点。

我们先让一个指针从头结点开始走到步到达第个结点，接着把指针放在头结点前的虚拟头结点，让二者同时向后遍历直至到达。这样，相当于跟着走了步， 也就到达了第个结点。我们删除其后的结点即可。

注意，这个虚拟头结点至关重要

  • 删除第一个结点，需要虚拟头结点
  • 从头结点开始走步，实际上到达了第个结点；从虚拟头结点开始走步，则是到达了第个结点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* dummy = new ListNode();
        dummy->next = head;

        ListNode* l = dummy;
        ListNode* r = head;

        for (int i = 0; i < n; i++) {
            r = r->next;
        }

        while(r) {
            r = r->next;
            l = l->next;
        }

        ListNode* tmp = l->next;
        l->next = tmp->next;
        ListNode* res = dummy->next;
        delete tmp;
        delete dummy;
        return res;
    }
};

链表的中间结点 - 876

给你单链表的头结点 head ，请你找出并返回链表的中间结点。

如果有两个中间结点，则返回第二个中间结点。

img
img

img
img

类似于上一题，我们希望在不统计链表结点总数的情况下解决这个问题，这里用到了快慢指针。

我们用两个指针从头开始遍历链表，其中每走一步，就走两步。当走到末尾时，则走到一半的位置。

同上一题，我们需要注意，如果从头节点开始，实际上默认已经走了一步，因此我们还是加个虚拟头节点，使得指针走的步长就等于链表结点的索引（从 1 开始）。

如何确保在有两个中间结点时返回第二个呢？我们只需要让在只能走一步时，仍然选择走一步即可。相当于（为奇数）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* middleNode(ListNode* head) {
        ListNode* dummy = new ListNode();
        dummy->next = head;
        ListNode* slow = dummy;
        ListNode* fast = dummy;

        while (fast) {
            fast = fast->next;
            fast = fast? fast->next: nullptr;
            slow = slow->next; 
        }

        return slow;
    }
};

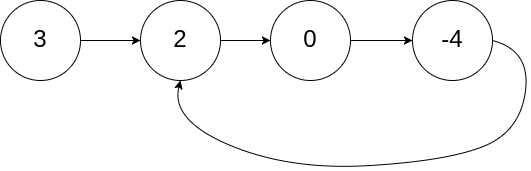
环形链表 II - 142

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

img
img

看到这题，我们首先要解决的问题是，如何判断链表是否有环呢？

说实话，我一开始实在是没有什么想法，然后就感受到了双指针的妙用。我们同样用和两个指针，前者每走一步后者就走两步（如果能走的话）。那么，假设有环的话，两个指针必然相遇。而且由于的速度是的二倍，所以当进入环后，其也必然在一圈内被追上。我们可能还会问，即使追上了，二者也未必在同一个位置吧？倘若在前一步，那下一次二者必然相遇；倘若在前两步，那下一次必然在前一步，再一次就会相遇。因此，我们可以通过判断二者能否相遇来判断是否有环。

成功判断环后，我们怎么找环的起点呢？

fig1
fig1

我们假设二者在紫色的点相遇，那么此时走了，在环内走了，除去从环的起点到相遇点走的长度，则有，则有。也就是说，只要再走，即可到达环的起点；而同样的，也是从头节点到环的起点的长度。那么，我们只要让回到起点，让二者以同样的速度前进，则二者的相遇点就是环的起点。

更直观的图如下：

img
img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {    
        ListNode* slow = head;
        ListNode* fast = head;
        while (fast != nullptr && fast->next != nullptr) {
            slow = slow->next;
            fast = fast->next->next;
            if (slow == fast) {
                slow = head;
                while(slow != fast) {
                    slow = slow->next;
                    fast = fast->next;
                }
                return slow;
            }
        }
        return nullptr;
    }
};

寻找重复数 - 287

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。

你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。

说来也是巧合，我在学习了上面的环形链表当晚，就在 B 站上刷到了这个题，也是狠狠地被秀到了。

看到这个找重复元素的问题，很自然的想法便是用个哈希表遍历数组，遇到重复元素就直接返回，但这个空间复杂度显然太高了。但进一步观察题干，中数字的范围都在，都刚好可以用来做数组的索引，也即每个元素都可单向对应到另一个元素。换言之，除了数组顺序这个比较自然的顺序外，中的元素还存在着另一种顺序关系。

考虑，结合上面的对应关系，则有下图

image-20250319195812253
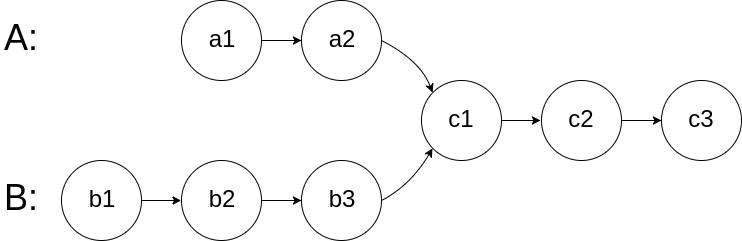
image-20250319195812253

我们发现，图中有三个链表。不难发现，导致链表出现回路的原因有三种：

  1. 自己指向自己
  2. 若干个元素循环依赖
  3. 出现重复元素（相当于原本一条链上有若干个值相同的点，将它们合并在一起形成环路）

（感觉这里面有不少的图论知识，但这里就不费脑筋证明了）

在上面的第三种情况中，重复元素同时为环路的起点，于是我们就可以把这个题转化为上面的环形链表起点问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int i = 0;
        int j = 0;
        do {
            i = nums[i];
            j = nums[nums[j]];
        } while(i != j);
        i = 0;
        while (i != j) {
            i = nums[i];
            j = nums[j];
        }
        return i;
    }
};

怎么保证我们找到的这个环路一定是重复元素所在的环路？因为我们从索引为的位置开始，而没有元素指向。

神奇吧？总有些算法，让我感到惊为天人……

相交链表 - 160

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

img
img

怎么判断两个链表是否相交呢？我们还会想到双指针，希望通过判断双指针是否相遇来判断是否相交。但问题在于，二者如何才能同步呢？一个很自然的想法是，先遍历两个链表获取其长度和，让长度较小者的指针先走步，即可使二者同步，问题便能很好地解决。

同样的，我们想怎么才能不用遍历两边呢？我们知道，二者相交部分的长度是一致的，差异在于不相交的部分，那我们只需要两个指针把两个链表不相交的部分都走一遍就自然同步了。于是我们得到如下解法：

  1. 两个链表各一个指针，从头节点出发
  2. 当指针走到空时，转到另一个链表的头节点
  3. 若二者相遇，则链表相交
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        ListNode* pA = headA;
        ListNode* pB = headB;

        while (pA != pB) {
            pA = pA == nullptr? headB: pA->next;
            pB = pB == nullptr? headA: pB->next;
        }
        return pA;
    }
};
推荐阅读
OS-Lab2 OS-Lab2 蓝桥杯学习笔记（一） 蓝桥杯学习笔记（一） 蓝桥杯学习笔记（二） 蓝桥杯学习笔记（二）
推荐阅读
OS-Lab2 OS-Lab2 蓝桥杯学习笔记（一） 蓝桥杯学习笔记（一）
目录
力扣刷题笔记（二）
  1. 1. 合并两个有序链表 - 21
  2. 2. 分隔链表 - 86
  3. 3. 合并 K 个升序链表 - 23
  4. 4. 删除链表的倒数第 个结点 - 19
  5. 5. 链表的中间结点 - 876
  6. 6. 环形链表 II - 142
  7. 7. 寻找重复数 - 287
  8. 8. 相交链表 - 160