力扣刷题笔记（一）

Foolish-Han Lv3
  2025-03-28 23:07:28 2025-03-28 23:07:28 创建   2025-03-28 23:07:28 2025-03-28 23:07:28 更新    2.3k 字  9 分钟  

我的日程安排表

实现一个 MyCalendar 类来存放你的日程安排。如果要添加的日程安排不会造成 重复预订 ，则可以存储这个新的日程安排。

当两个日程安排有一些时间上的交叉时（例如两个日程安排都在同一时间内），就会产生 重复预订 。

日程可以用一对整数 startTime 和 endTime 表示，这里的时间是半开区间，即 [startTime, endTime), 实数 x 的范围为， startTime <= x < endTime 。

实现 MyCalendar 类：

  • MyCalendar() 初始化日历对象。
  • boolean book(int startTime, int endTime) 如果可以将日程安排成功添加到日历中而不会导致重复预订，返回 true 。否则，返回 false 并且不要将该日程安排添加到日历中。

这个题挺有意思的，学到了许多不同的解法，特此记录一下。

二分查找

基本思路比较简单，我们用动态数组维护已经预定的日程，并保持按照有序。当我们要插入一个新的日程时，我们先找到中的的（起始时间不小于 s 的第一个元素）和的前驱元素，则只要满足且即可插入数组。

具体的代码中，我们使用 set 来保证有序性。pair 的比较规则则是按照字典序。当然，由于左右边界可能不存在的情况，我们需要考虑繁杂的边界条件。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class MyCalendar {
    set<pair<int, int>> record;

public:
    MyCalendar() {
        
    }
    

    bool book(int startTime, int endTime) {
        auto iter = record.lower_bound({startTime, endTime});
        if ((iter == record.end() && (record.empty() || prev(iter)->second <= startTime)) || 
        (endTime <= iter->first && (iter == record.begin() || prev(iter)->second <= startTime))) {
            record.insert({startTime, endTime});
            return true;
        } 
        return false;
    }
};

为了避免耗费脑力考虑边界，我们可以根据数据范围，提前插入一对保证不会影响其他日程安排的边界。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class MyCalendar {
    set<pair<int, int>> record;

public:
    MyCalendar() {
        record.insert({-1, 0});
        record.insert({1e9, 1e9+1});
    }

    bool book(int startTime, int endTime) {
        auto iter = record.lower_bound({startTime, endTime});
        if (prev(iter)->second <= startTime && endTime <= iter->first) {
            record.insert({startTime, endTime});
            return true;
        } 
        return false;
    }
};

这个方法确实比较简单、高效，但相对的，在题目要求变化时就无法派上用场。

线段树

实现一个程序来存放你的日程安排。如果要添加的时间内不会导致三重预订时，则可以存储这个新的日程安排。

当三个日程安排有一些时间上的交叉时（例如三个日程安排都在同一时间内），就会产生 三重预订。

事件能够用一对整数 startTime 和 endTime 表示，在一个半开区间的时间 [startTime, endTime) 上预定。实数 x 的范围为 startTime <= x < endTime。

实现 MyCalendarTwo 类：

  • MyCalendarTwo() 初始化日历对象。
  • boolean book(int startTime, int endTime) 如果可以将日程安排成功添加到日历中而不会导致三重预订，返回 true。否则，返回 false 并且不要将该日程安排添加到日历中。

现在题目进行了升级，可以进行二重预定而不能进行三重预订。一个很通用的方法是 线段树，我们记录每个时间点被预订的次数。但是由于时间范围非常大（），我们不可能把这么多叶子节点都存储起来，因此我们使用 unordered_map<int, int> 来记录每个时间点的预订次数。

cpp 在使用一个表中不存在的 key 时，会自动创建这个键并将其值初始化为默认值，因此所有我们未添加到键值对都视为预订次数为。

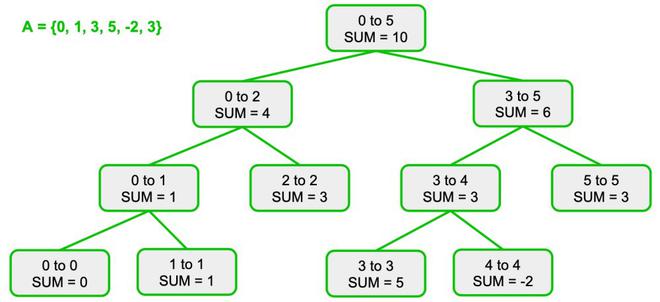
在这里，为了进行加速，我使用了懒更新来优化。即在为某一段区间更新值时，并不更新区间中的所有非叶结点和叶节点，而是只更新到最顶层的父结点，同时标记其直接子结点的 lazy，表面子节点现存的值未更新，只在查询或更新的颗粒度达到需要子节点的值时才向下传递一层。

img
img

比如要给区间的所有值加一，那么就只更新对应的非叶节点的值，同时标记其子节点的 lazy。只有当我们查询或更新需要用到其子节点时，我们才把 lazy 清零并添加给子节点，同时把 lazy 向子节点的子节点传播。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
class MyCalendarTwo {
    unordered_map<int, int> tree, lazy;

   public:
    MyCalendarTwo() {}

    bool query(int start, int end, int l, int r, int idx) {
        if (lazy[idx] > 0) {
            tree[idx] += lazy[idx];
            if (l != r) {
                lazy[2 * idx] += lazy[idx];
                lazy[2 * idx + 1] += lazy[idx];
            }
            lazy[idx] = 0;
        }

        if (start > end || r < start || end < l) {
            return false;
        }

        if (start <= l && r <= end) {
            return tree[idx] > 1;
        }

        int mid = (l + r) >> 1;
        return query(start, end, l, mid, 2 * idx) ||
               query(start, end, mid + 1, r, 2 * idx + 1);
    }

    void update(int start, int end, int l, int r, int idx) {
        if (lazy[idx] > 0) {
            tree[idx] += lazy[idx];
            if (l != r) {
                lazy[2 * idx] += lazy[idx];
                lazy[2 * idx + 1] += lazy[idx];
            }
            lazy[idx] = 0;
        }

        if (start > end || r < start || end < l) {
            return;
        }

        if ( start <= l && r <= end) {
            tree[idx]++;
            if (l != r) {
                lazy[2 * idx] += 1;
                lazy[2 * idx + 1] += 1;
            }
            return;
        }

        int mid = (l + r) >> 1;
        update(start, end, l, mid, 2 * idx);
        update(start, end, mid + 1, r, 2 * idx + 1);
        tree[idx] = max(tree[2 * idx], tree[2 * idx + 1]);
    }

    bool book(int startTime, int endTime) {
        if (query(startTime, endTime - 1, 0, 1e9, 1)) {
            return false;
        }
        update(startTime, endTime - 1, 0, 1e9, 1);
        return true;
    }
};

但是这个题比较麻烦的是，由于时间的范围 C 比较大，输入的规模 n 却又相对比较小，哈希表的常数级开销又比较大。导致尽管线段树的复杂度为，但实际运行效率却要比下面这种的朴素遍历方法差得多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class MyCalendarTwo {
private:
    vector<pair<int, int>> booked;
    vector<pair<int, int>> overlaps;
public:
    MyCalendarTwo() {
        
    }
    
    bool book(int startTime, int endTime) {
        for (auto &[l, r] : overlaps) {
            if (l < endTime && r > startTime)
                return false;
        }
        for (auto &[l, r] : booked) {
            if (l < endTime && r > startTime)
                overlaps.emplace_back(max(l, startTime), min(r, endTime));
        }
        booked.emplace_back(startTime, endTime);
        return true;
    }
};

差分数组

说到这里，我们就得提到这个题比较优雅的解法，差分数组。同样的，为了避免空间开销过大，我们仍然使用哈希表来记录，使得未添加的元素默认未零。但需要注意的是，由于差分需要保证有序性，因此我们使用能够保证按照 key 有序排列的 map 而非 unordered_map。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class MyCalendarTwo {
public:
    MyCalendarTwo() {

    }

    bool book(int start, int end) {
        int maxBook = 0;
        cnt[start]++;
        cnt[end]--;
        for (auto &[_, freq] : cnt) {
            maxBook += freq;
            if (maxBook > 2) {
                cnt[start]--;
                cnt[end]++;
                return false;
            }
        }
        return true;
    }
private:
    map<int, int> cnt;
};

可以看到，差分方法的时间复杂度仍然是，甚至实际上由于哈希表的缘故效率要低得多。但这种方法比较好的地方在于，我们可以解决任意重区间预订的问题而不限于两重，朴素遍历方法则需要手写重遍历逻辑。

二分查找

看样子，上面的做法已经很厉害了，似乎没有更优越的算法了。然而，总有一些算法让我感觉惊为天人。

我们在使用线段树时，为了维护庞大的树形结构，就无可避免地有了的复杂度。我们能不能把这个优化一下呢？我们用表示时间点共有次预订。那么：

在查询某个时间段的最大预订次数时，我们只需要遍历的预订次数即可。其中是不大于的最大数，是小于的最大数。换句话说，是或其左边第一个数，是左边第一个数。

在为某个时间段增加预订次数时，如果和已经在哈希表中，我们将表中的预订次数加一即可；如果或不在表中，我们就首先需要计算或处的预订次数。那么类似的，和的预定次数都应该与其左边第一个数一致。我们先把或创建并初始化出来，然后再进行同样的遍历自增操作即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class MyCalendarTwo {
public:
    MyCalendarTwo() {
        book_.emplace(0, 0);       // 初始化左边界
        book_.emplace(INT_MAX, 0); // 初始化右边界
    }

    // 插入事件
    void add(int startTime, int endTime) {
        auto iter0 = book_.upper_bound(startTime);
        --iter0;
        auto iter1 = book_.upper_bound(endTime);
        --iter1;

        // 拆分区间
        if (startTime > iter0->first) {
            book_.emplace(startTime, iter0->second);
        }
        if (endTime > iter1->first) {
            book_.emplace(endTime, iter1->second);
        }

        // 更新事件计数
        for (auto iter = book_.lower_bound(startTime); iter != book_.end() && iter->first < endTime; ++iter) {
            ++(iter->second);
        }
    }

    // 查询区间 [queryStart, queryEnd) 内的最大预订次数
    int queryMax(int queryStart, int queryEnd) {
        int maxCount = 0;
        auto iterStart = book_.upper_bound(queryStart);
        iterStart--;
        auto iterEnd = book_.lower_bound(queryEnd);

        // 遍历 [queryStart, queryEnd) 区间内的所有时间点
        for (auto iter = iterStart; iter != iterEnd; ++iter) {
            maxCount = std::max(maxCount, iter->second);
        }

        return maxCount;
    }

    bool book(int startTime, int endTime) {
        if (queryMax(startTime, endTime) > 1) {
            return false;
        } else {
            add(startTime, endTime);
            return true;
        }
    }

private:
    std::map<int, int> book_; // 时间点 -> 事件计数
};

关于 lower_bound 和 upper_bound:

  1. 不小于：lower_bound
  2. 大于：upper_bound
  3. 不大于：prev(upper_bound)
  4. 小于: prev(lower_bound)
推荐阅读
蓝桥杯学习笔记（一） 蓝桥杯学习笔记（一） 蓝桥杯学习笔记（二） 蓝桥杯学习笔记（二） OS-Shell Challenge OS-Shell Challenge
推荐阅读
蓝桥杯学习笔记（一） 蓝桥杯学习笔记（一） 蓝桥杯学习笔记（二） 蓝桥杯学习笔记（二）
目录
力扣刷题笔记（一）
  1. 1. 我的日程安排表
    1. 1.1. 二分查找
    2. 1.2. 线段树
    3. 1.3. 差分数组
    4. 1.4. 二分查找